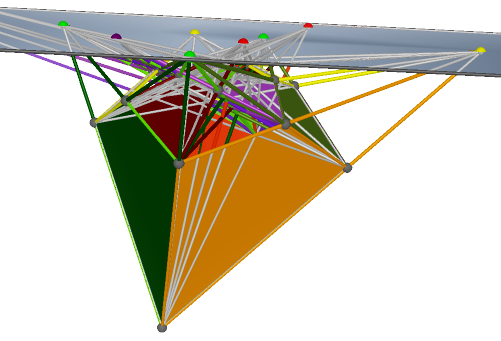
Reye's Configuration on A'n and Properties |
|---|
Reye’s Configuration on 
and properties
In character 3, we have done 
from 
by inversion for 
.The compatibility of them
is
that they all have quadrilaterals. So we have the first property here:
Prop. 1 Two quadrilaterals on form a Reye’s configuration if and only if they come from two
parallel squares on , for 
. Actually, only for 
and 
, since others but
has no
square.
|
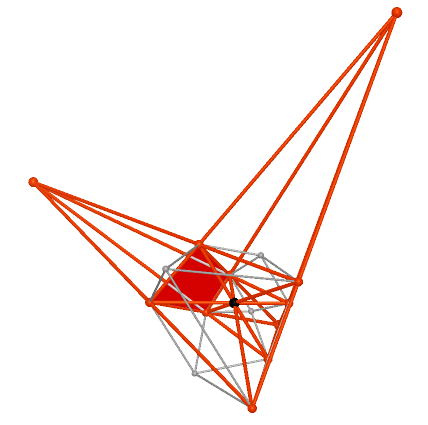
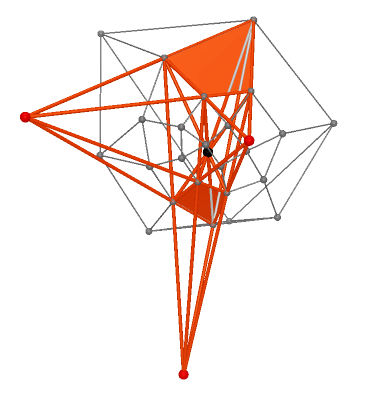
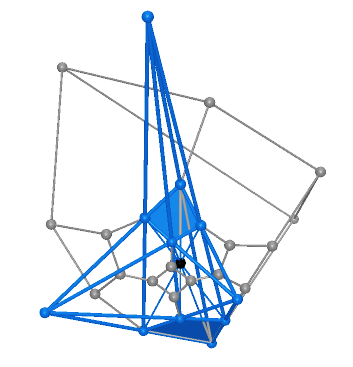
Figure 4.1 |
|
Figure 4.2 |
|
Figure 4.3 |
|
Figure 4.4 |
|
Figure 4.5 |
|
Figure 4.6 |
Prop. 2 The multiplicity of each center of perspectivity which is used by different Reye’s configuration
on each is below:
(1) For 
, every centers of perspectivity is only used for one Reye’s configurations. Hence
the multiplicity is 1.
(2) For 
, 6 Reye’s configurations can be divided into 3 groups consisting 2 Reye’s configurations,
each group share 3 centers of perspectivity. Hence the multiplicity is 2.
(3) For 
, 15 Reye’s configurations can be divided into 5 groups consisting 3 Reye’s configurations.
Each group shares 3 centers of perspectivity. Hence the multiplicity is 3.
(4) For 
, 9 Reye’s configurations can be viewed into 2 groups. One has 3 Reye’s configurations
sharing 3 centers of perspectivity; and the other has 6 Reye’s configurations, and it can be divided into
3 subgroups consisting 2 Reye’s configurations, each subgroup share 3 centers of perspectivity which
are shared by the first group. Hence 3 centers of perspectivity are shared by 5 Reye’s configurations,
and
6 centers of perspectivity are shared by 2 Reye’s configurations. So the multiplicity of 3 centers of
perspectivity
is 5, and the multiplicity of other 6 centers of perspectivity is 2.
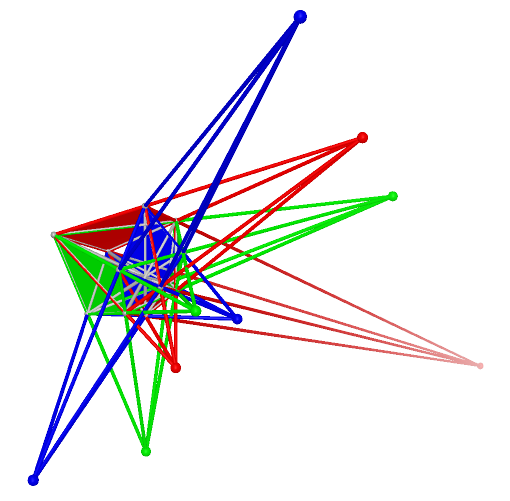
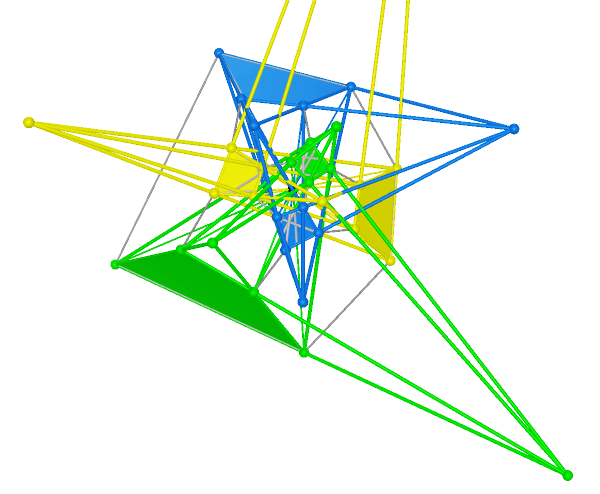
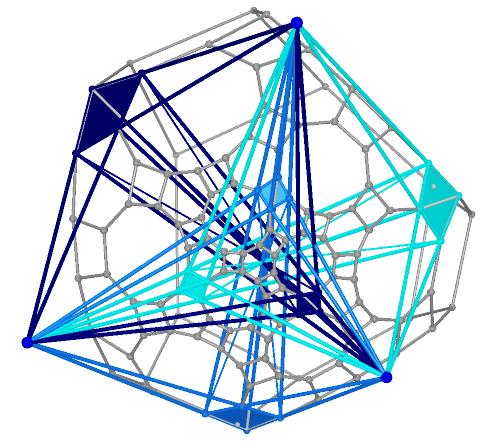
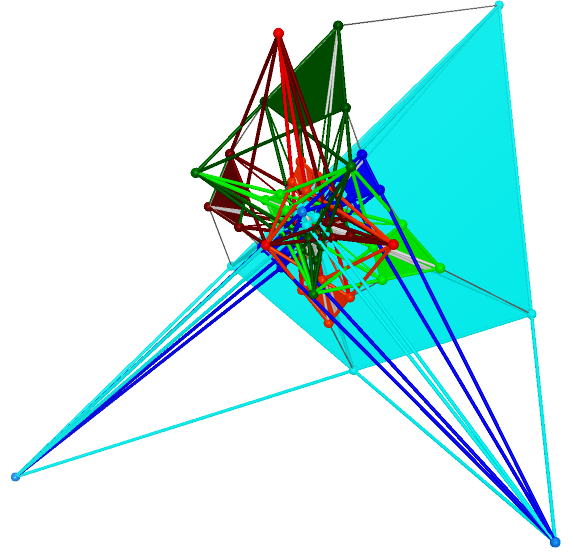
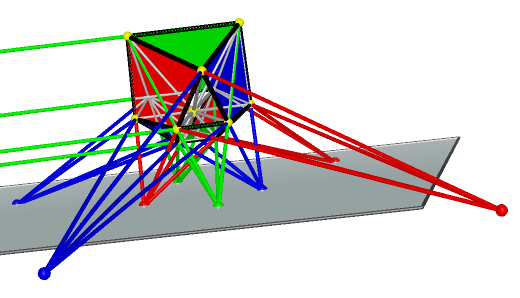
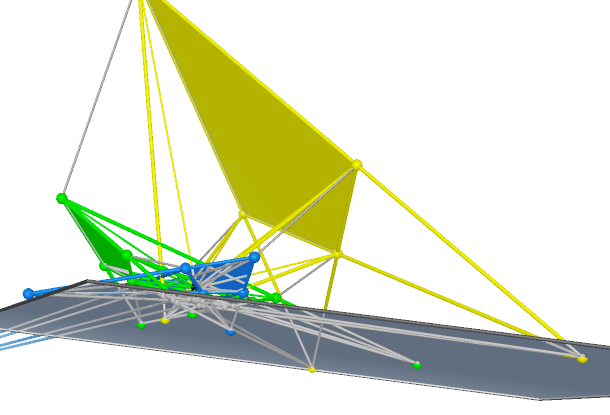
For a better view of this property, we set the Reye’s Configurations which use same perspectivities by
similar colors. If two Reye’s Configurations do not share any perceptivities, they are in different colors.
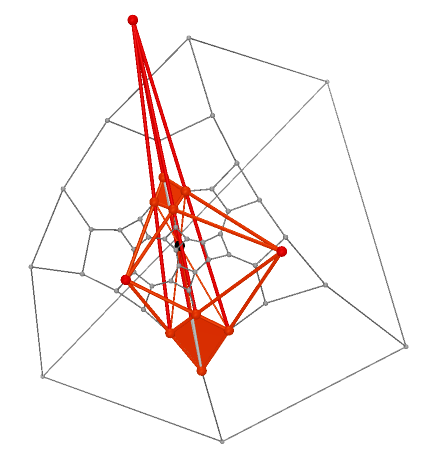
multiplicity is 1 |
|
|
|
|
|
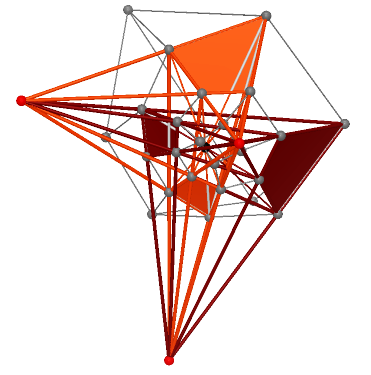
multiplicity is 2 |
|
|
multiplicity is 3 |
|
|
multiplicity is 3 |
|
|
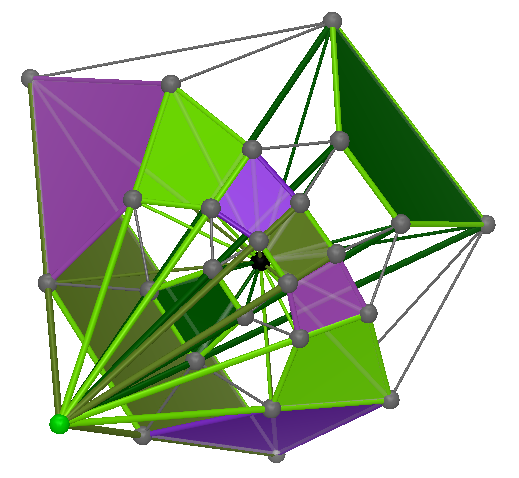
multiplicity is (5,2) |
|
|
multiplicity is (5,2) |
|
|
|
|
|
|
|
|
|
|
3 |
6 |
||||||
multiplicity of the centers of perspectivity |
1 |
3 |
2 |
3 |
5 |
2 |
1 |
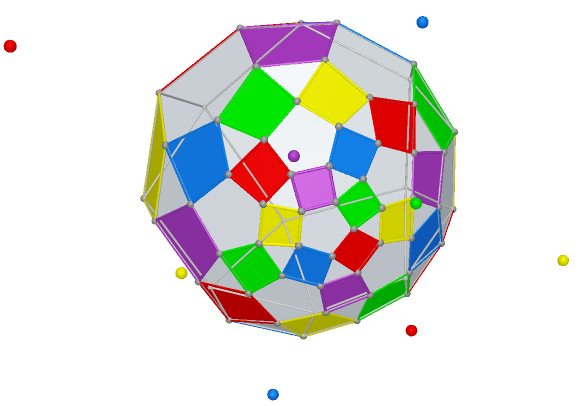
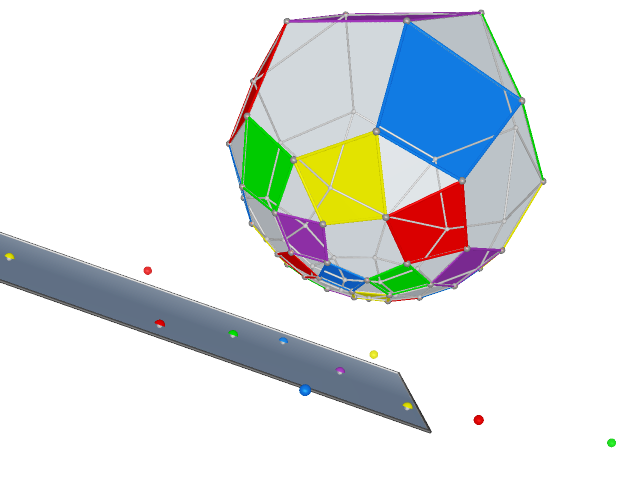
Prop. 3 The number of Reye’s configurations in equals to the number of all centers of perspectivity
for 
. We have the number table and graph table below:
|
|
|
|
|
|
|
number of Reye’s configurations |
3 |
15 |
6 |
15 |
9 |
3 |
number of centers of perspectivity |
9 |
15 |
9 |
15 |
9 |
9 |
|
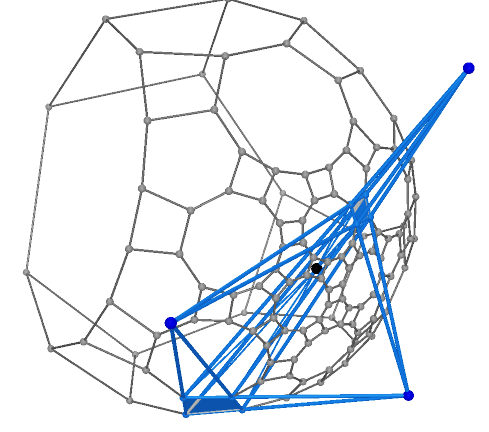
Figure 4.14 |
|
Figure 4.15 |
|
Figure 4.16 |
|
Figure 4.17 |
|
Figure 4.18 |
|
Figure 4.19 |
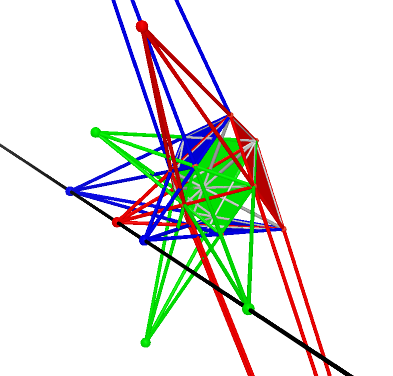
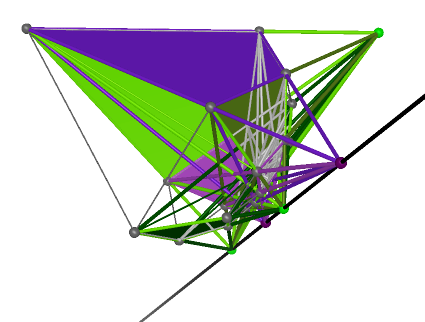
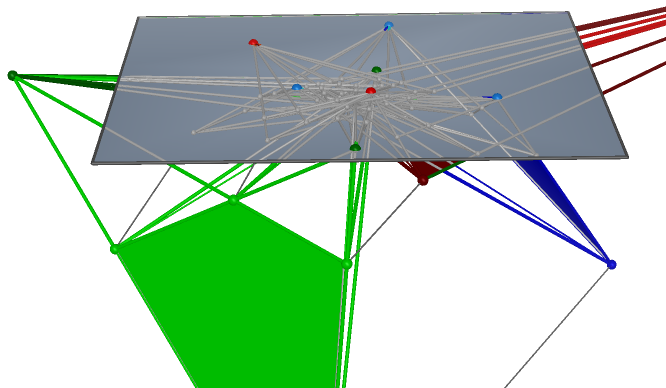
Prop. 4 The maximum of collinear centers of perspectivity in Reye’s configurations from :
(1) For 
, all 3 centers of perspectivity in Reye’s configurations are collinear, so the maximum
of collinear centers of perspectivity is 3.
(2) For , 2 real centers of perspectivity in one group( see Prop. 2(2) ) and each unreal center
of perspectivity in other two groups, the four points are collinear. So the maximum of collinear
centers of perspectivity is 4.
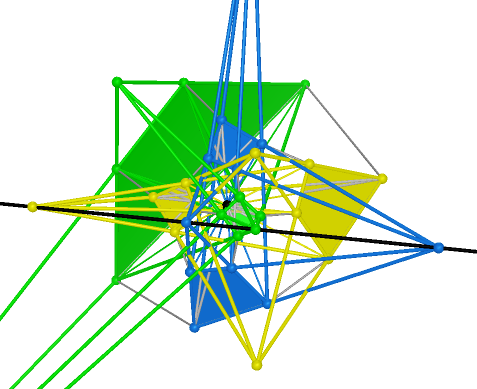
(3) For , 2 real centers in the second group( see Prop. 2(4) ) and 2 centers in the first group,
the four points are collinear. So the maximum of collinear centers of perspectivity is 4.
(4) For 
, 2 unreal centers of perspectivity in one Reye’s configuration and each real centers of
perspectivity in other two Reye’s configurations, the four points are collinear. So the maximum
of collinear centers of perspectivity is 4.
(5) For 
, 5 centers of perspectivity in different groups( see Prop. 2(3) ) are collinear. So the
maximum of collinear centers of perspectivity is 5.
We use black color to show the collinearity. The graph table is below:
|
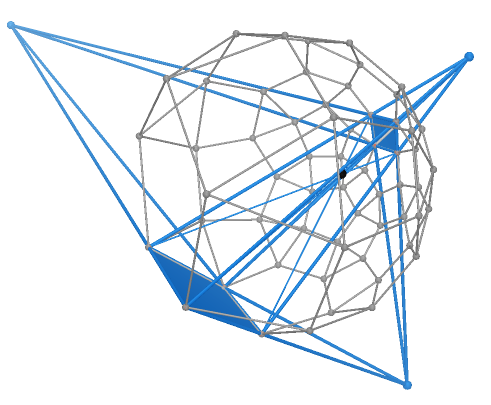
Maximum of collinear centers of perspectivity |
Collinearity |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
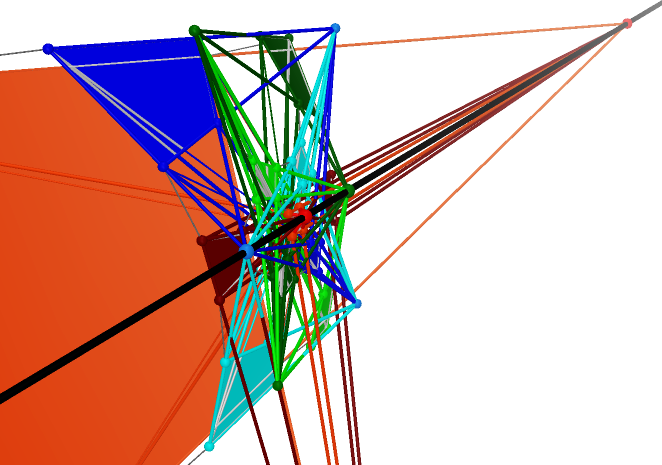
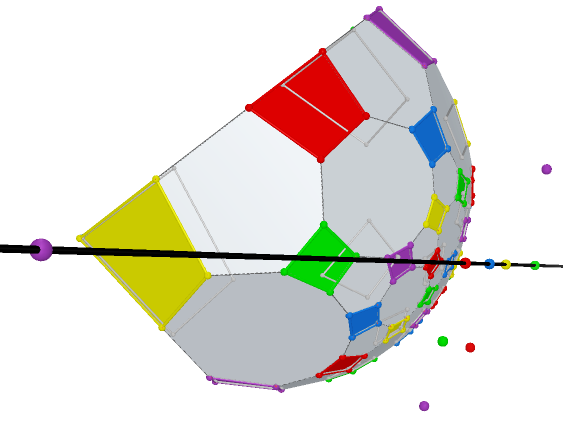
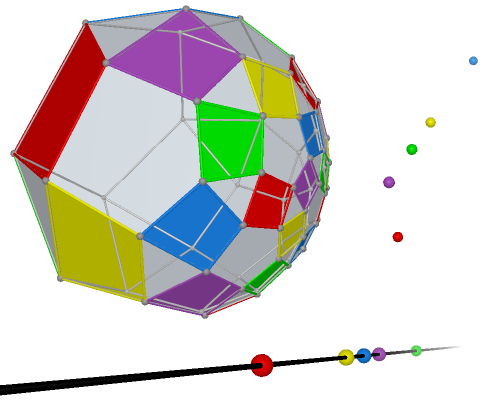
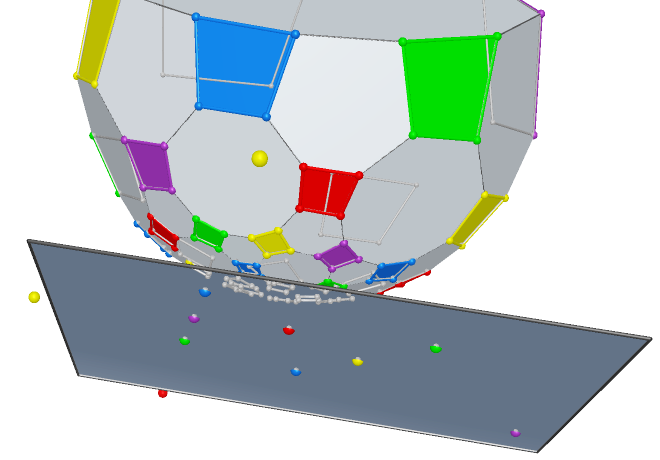
Prop. 5 All centers of perspectivity of all Reye’s configurations are coplanar for each ,
.
The graph table is below:
|
|
|
|
|
|
|
|
|
|
|
|
