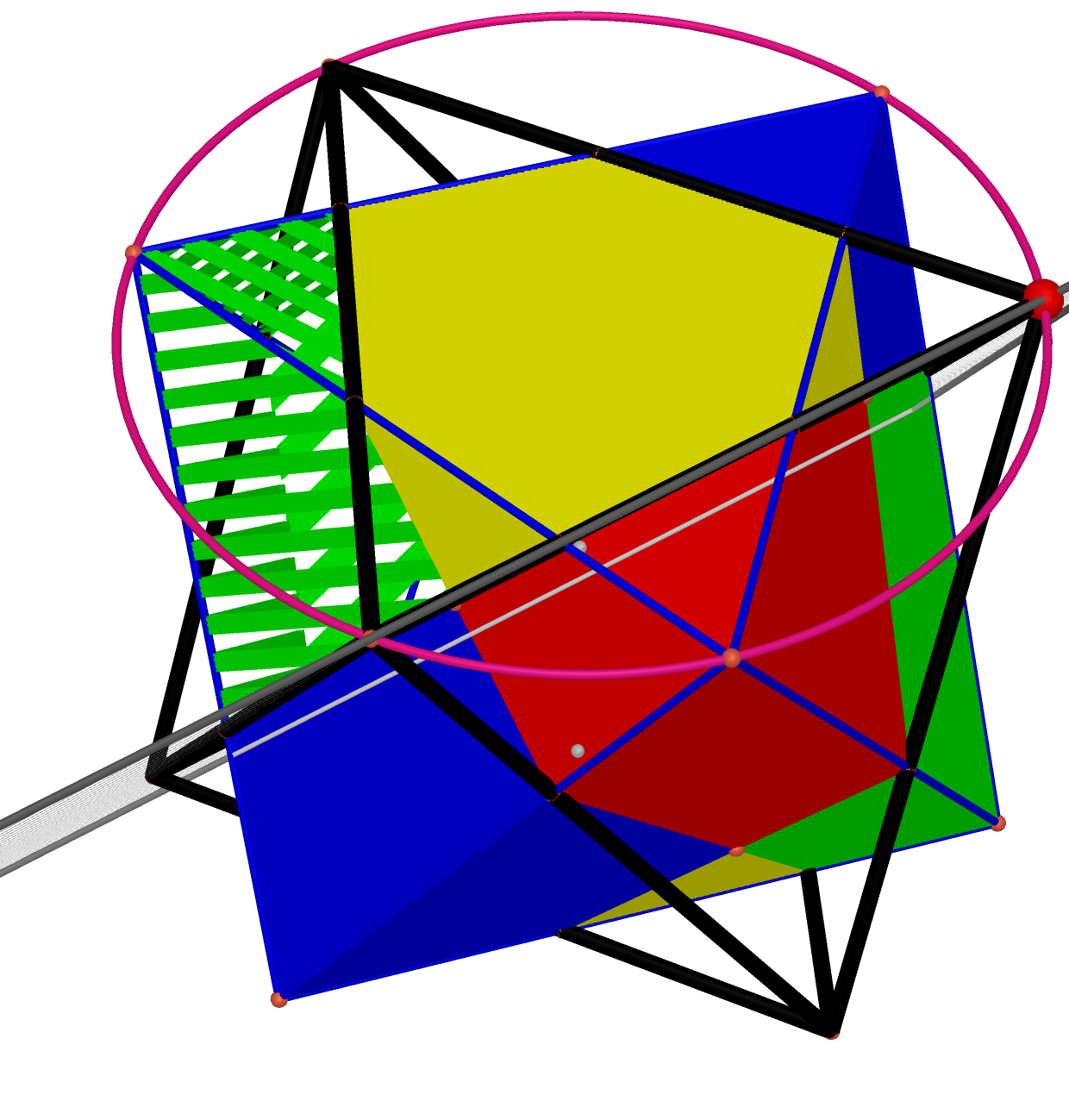
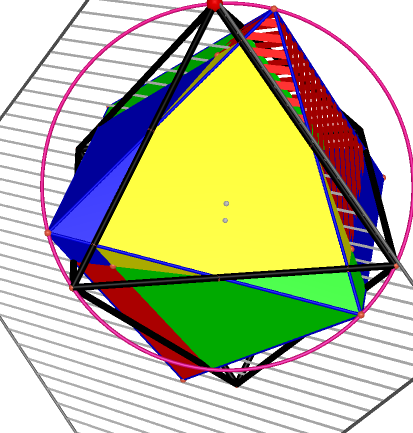
The following are four steps could construct the self-projection polygon: (Click Here to See The Dynamic Process)
Step 1. Rotated the original polygon around the symmetric axis.
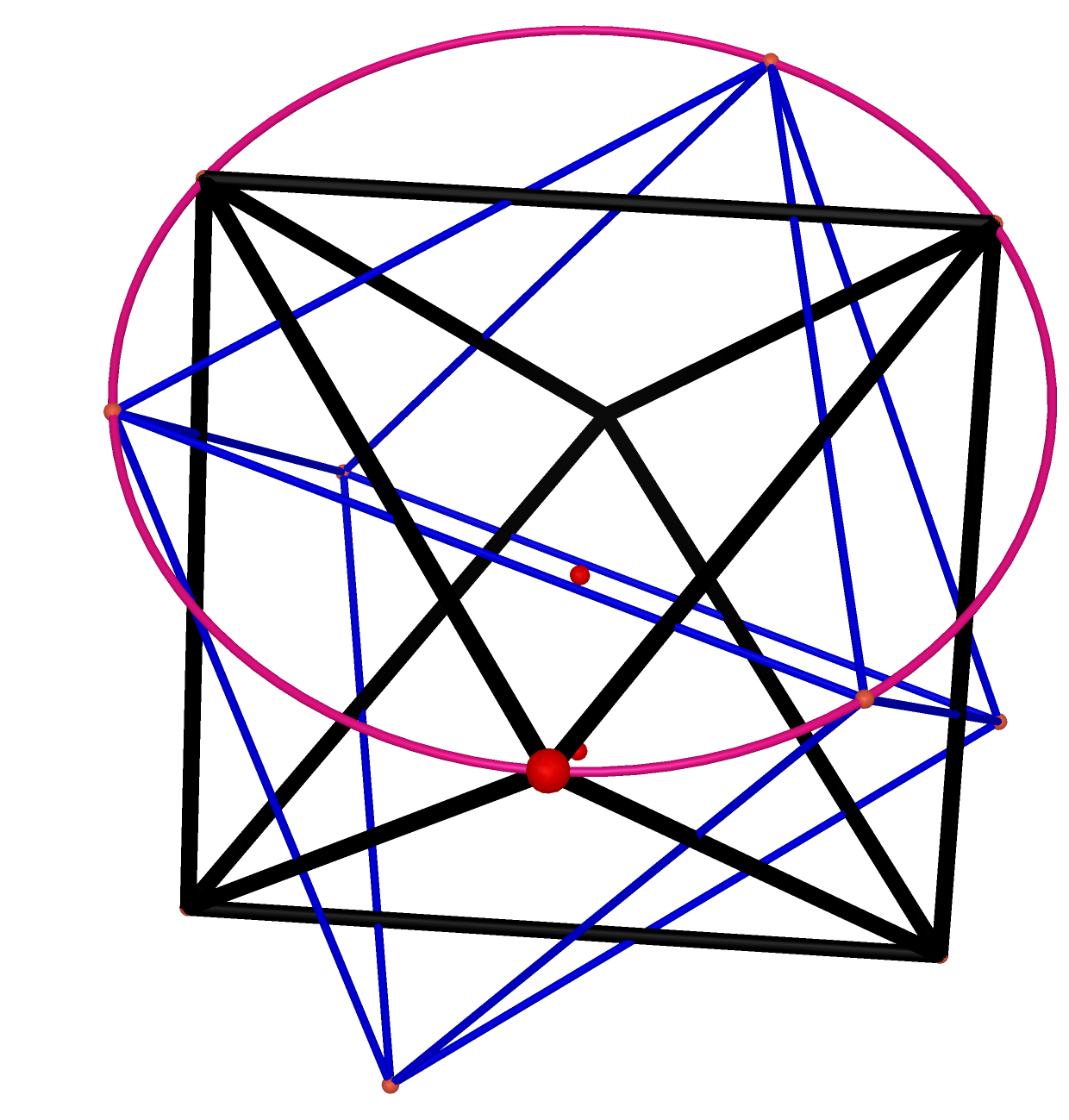
Step 2. Construct the splitter with one face and the center of the polygon.
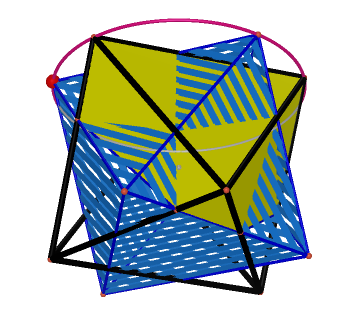
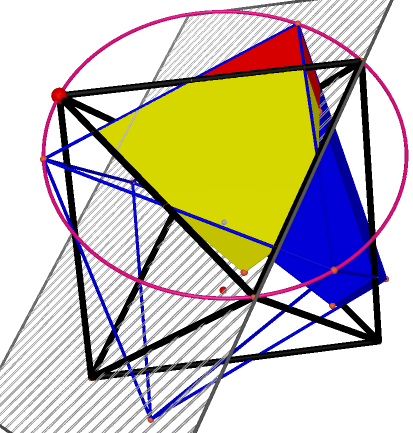
Select half of the rotated octahedron and the center face inside of it and then construct a convex hull composed with. This constructed convex hull is a pyramid which is irregular. The height of it is This irregular pyramid is seemed as a splitter, which cut the original octahedron into component. Because the interface between it and the original octahedron is the projection of the rotated octahedron, which was prooved by linear matrix equation. |
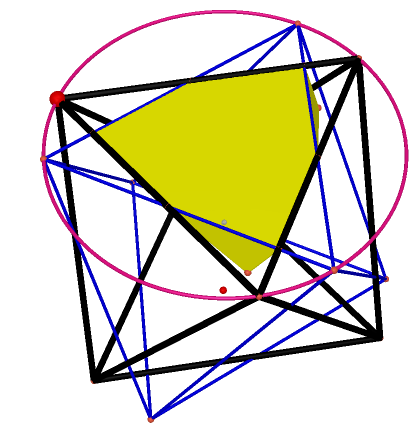
Step 3. Construct the projection component with cutting the original polygon with the splitter.
We cut the original octahedron with the splitter which metioned in the Step 2. The polygon with yellow faces is what we construct after splitting. And the face will change when the vertex of rotated octahedron rotating, which shows the projected surface. We see this resulted polygon as a component which combine a new octahedron because of symmetry. |
Step 4. Duplicate the projection component with Axisymmetric or Pointsymmetric.
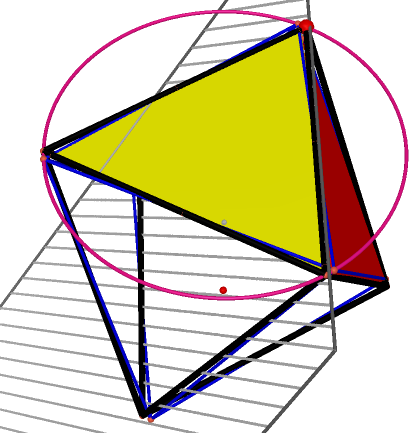
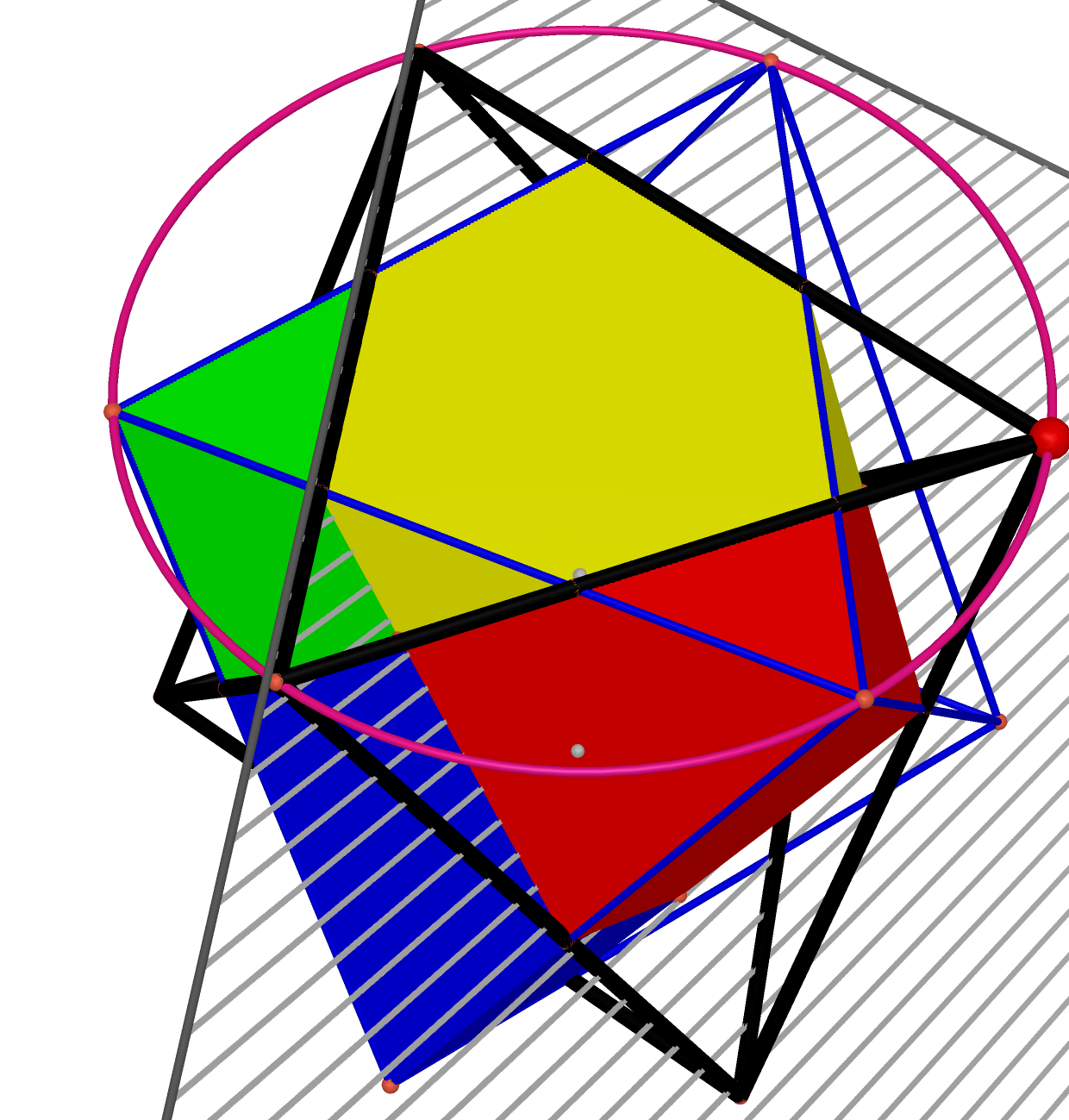
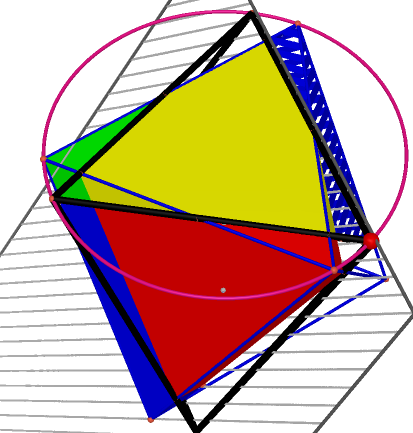
Then we start to duplicate the component with symmetric properties of octahedron. First, the polygon with red surfaces by the yellow one counter the plane centered the octahedron, which concludes 4 sides of the octahedron. This is also the axisymmetric of reflection. |
And then is the polygon with blue surfaces, which was duplicated with the same way but different plane. |
Repeat the step above and then duplicate the green one. These four component combine the top half of the octahedron. |
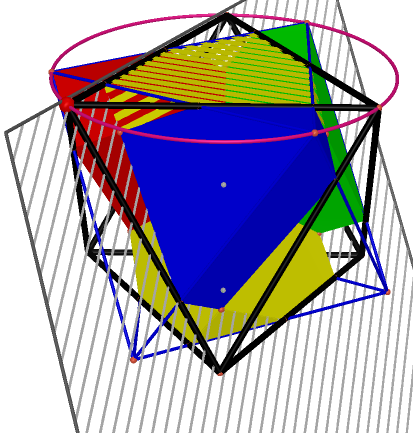
Because of the resulted polygon mentioned above, we can easily duplicate the buttom half of the octahedron by point symmetric. First if the blue one, which is duplicated by the other blue one marked with stripes. |
And then is the yellow one, using the same method mentioned above. |
Also the polygon with green surfaces. |
Finally is the polygon with red surfaces. Then we can construct the final result: the projection of a rotated octahedron on the original octahedron. |
To see other prove of the symmetric properties, click Here.