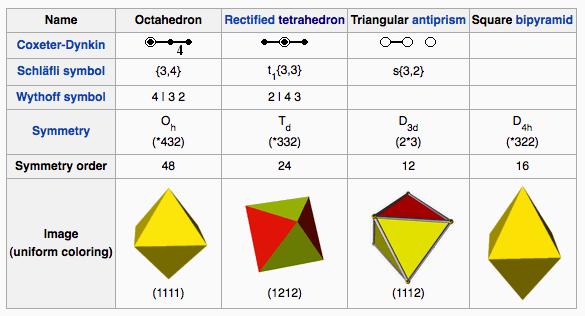
If the edges of an octahedron are divided in the golden ratio such that the points of division for any face form an equilateral triangle, then the twelve points of division form an icosahedron (Wells 1991).

In fact, there are two ways in which the edges can be internally divided in the golden ratio and two ways in which they can be externally divided, resulting in four possible icosahedra.

Keeping the same connectivity, but reversing the long and short ends of the division gives Jessen's orthogonal icosahedron.

A plane perpendicular to a axis of an octahedron cuts the solid in a regular hexagonal cross section (Holden 1991, pp. 22-23).

Since there are four such axes, there are four possible hexagonal cross sections.

Uniform colorings and symmetry

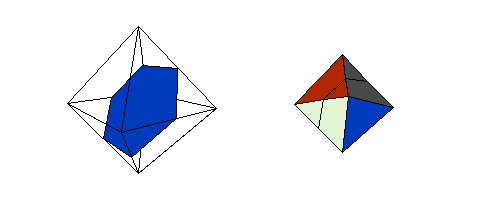
There are 3 uniform colorings of the octahedron, named by the triangular face colors going around each vertex: 1212, 1112, 1111.

The octahedron's symmetry group is Oh, of order 48, the three dimensional hyperoctahedral group.

This group's subgroups include D3d (order 12), the symmetry group of a triangular antiprism; D4h (order 16), the symmetry group of a square bipyramid; and Td (order 24), the symmetry group of a rectified tetrahedron.

These symmetries can be emphasized by different colorings of the faces.