新增網頁3

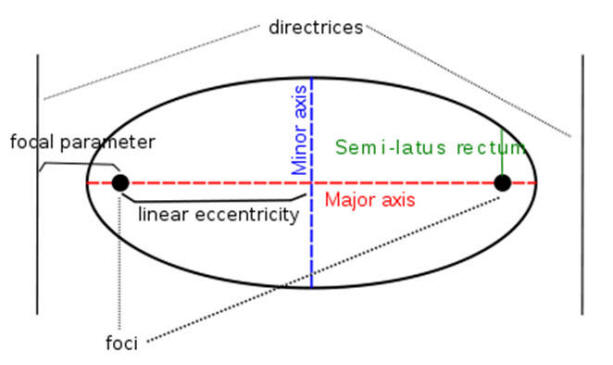
Conic sections are exactly those curves that, for a point F, a line L not containing F and a non-negative number e, are the locus of points whose distance to F equals e times their distance to L. F is called the focus, L the directrix, and e the eccentricity.

The linear eccentricity (c) is the distance between the center and the focus (or one of the two foci).
The latus rectum (2ℓ) is the chord parallel to the directrix and passing through the focus (or one of the two foci).
The semi-latus rectum (ℓ) is half the latus rectum.
The focal parameter (p) is the distance from the focus (or one of the two foci) to the directrix.
　

The following relations hold：

pe = l
ae = c
　

conic section	equation	eccentricity (e)	linear eccentricity (c)	semi-latus rectum (ℓ)	focal parameter (p)
circle	$x^2+y^2=a^2 \,$	$0 \,$	$0 \,$	$a \,$	$\infty$
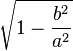ellipse	$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$	$\sqrt{1-\frac{b^2}{a^2}}$	$\sqrt{a^2-b^2}$	$\frac{b^2}{a}$	$\frac{b^2}{\sqrt{a^2-b^2}}$
parabola	$y^2=4ax \,$	$1 \,$	$a \,$	$2a \,$	$2a \,$
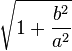hyperbola	$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$	$\sqrt{1+\frac{b^2}{a^2}}$	$\sqrt{a^2+b^2}$	$\frac{b^2}{a}$	$\frac{b^2}{\sqrt{a^2+b^2}}$