| |
Inverslization
Wang-Hsiuan Pahngerei
2013.06.24
There're two usual ways to ``go" from a magma to a group, as the diagram below,

where ``divisibility" means for any 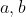 , ,  and and 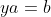 admits a unique solution. admits a unique solution.
Recall that a monoid is a pair ) such that such that  is associative and has an identity is associative and has an identity  . Elements of a monoid need not have an inverse, so we hope to ``extend" it to a group in some conditions. In fact, this action helps us contruct the Zahlen from the set of natural numbers. . Elements of a monoid need not have an inverse, so we hope to ``extend" it to a group in some conditions. In fact, this action helps us contruct the Zahlen from the set of natural numbers.
Let us focus on commutative monoids with cancellation law (i.e.  implies implies 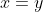 ). In fact, this is really near a group. Firstly, define a relation ). In fact, this is really near a group. Firstly, define a relation 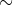 on on  by by \sim(x,y)) if and only if if and only if  . This is an equivalence relation because, (i) . This is an equivalence relation because, (i)  so so \sim(a,b)) , (ii) , (ii) \sim%20(c,d)) means means  , so , so  , that is , that is \sim%20(a,b)) , and , and ) whenever whenever \sim(c,d)\sim(e,f)) , ,  and and  , so , so  , indicating , indicating  . .
Secondly, let 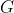 be the set of equivalence classes. Then we define operation: be the set of equivalence classes. Then we define operation: ]%20\ast%20[(x,y)]%20=%20[(%20a\ast%20x,%20b\ast%20y)]) . This is well-defined because, written . This is well-defined because, written \sim%20(a',b')) and and \sim%20(x',%20y')) , so we have , so we have
 . .
Thirdly, ]) is the identity of the new ``group", and for is the identity of the new ``group", and for ]\in%20G) , , ]) is the inverse. We're going to show that is the inverse. We're going to show that  by by ]) is the embedding (one-to-one monoid homomorphism). It's enough to show that is the embedding (one-to-one monoid homomorphism). It's enough to show that 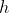 is one-to-one, but this is routine because is one-to-one, but this is routine because ]=%20[(1,b)]) implies implies  . .
\text{ }
Now we hope to add in another operation. Recall that a semiring is a pair ) such that such that ) is a commutative monoid with identity is a commutative monoid with identity 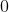 , , ) is a monoid with identity is a monoid with identity 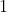 , it has both side multiplicative distrubution over addition, and multiplication by , it has both side multiplicative distrubution over addition, and multiplication by 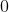 annihilates annihilates 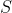 ( ( ). We now consider a commutative semiring ). We now consider a commutative semiring ) . .

Let ) be the equivalence classes as mentioned above. We hope to add multiplication so that be the equivalence classes as mentioned above. We hope to add multiplication so that ) is a ring. Define is a ring. Define
]\cdot[(x,y)]%20=%20[(%20ay%2Bbx,%20ax%2Bby%20)].\notag%20\end{align})
It's routine to check well-defined. If \sim%20(a',b')) and and \sim(x',y')) , then , then
(a'x'%2Bb'y')%20&=%20aa'yx'%20%2B%20yy'ab'%20%2B%20xx'ba'%20%2B%20bb'xy'%20\notag\\%20&=%20aa'xy'%20%2B%20yy'a'b%20%2B%20xx'ab'%20%2B%20bb'x'y%20=%20(a'y'%2Bb'x')(ax%2Bby).\notag%20\end{align})
Note that the mapping 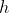 is again an embedding. Thus we view is again an embedding. Thus we view 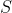 as a semi-subring of as a semi-subring of 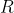 . Again, throughout this method, we have the conclusion that . Again, throughout this method, we have the conclusion that  . .
|
|