Chapter 2 : Classification
2.1 Axes and Centers
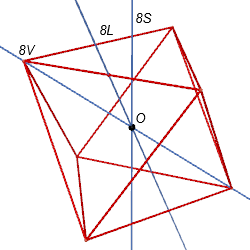
Through observing the previous figure, we find the projection is related by the axes of two Platonic solids, so we have to observe the axes of Platonic solids first. For example, there lists all axes and the center of an octahedron.
 |
 |
 |
 |
| 2-fold axis 8L | 3-fold axis 8S | 4-fold axis 8V | center |
2.2 Rotation Group
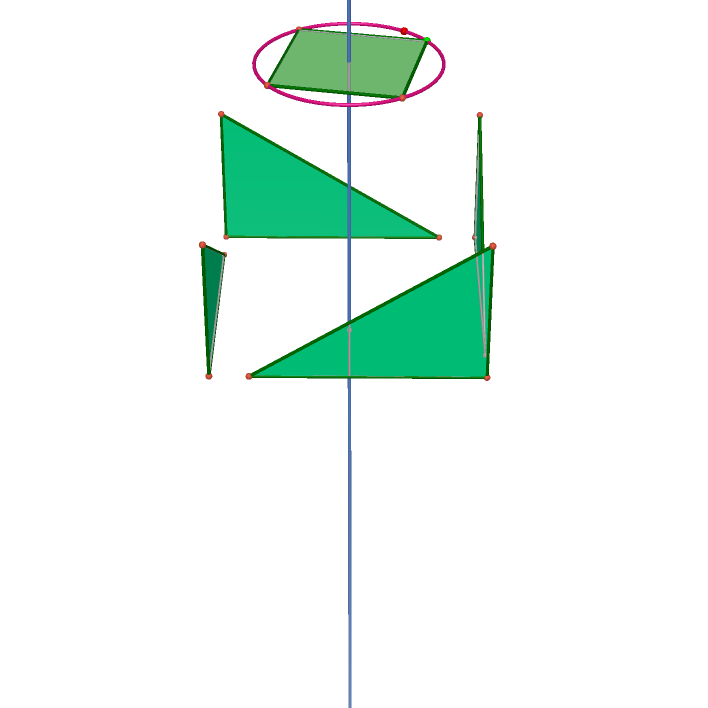
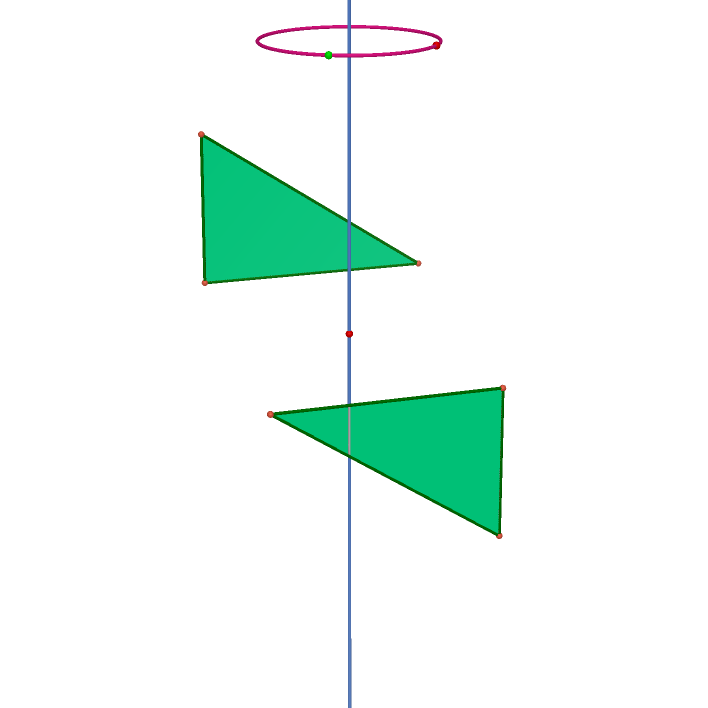
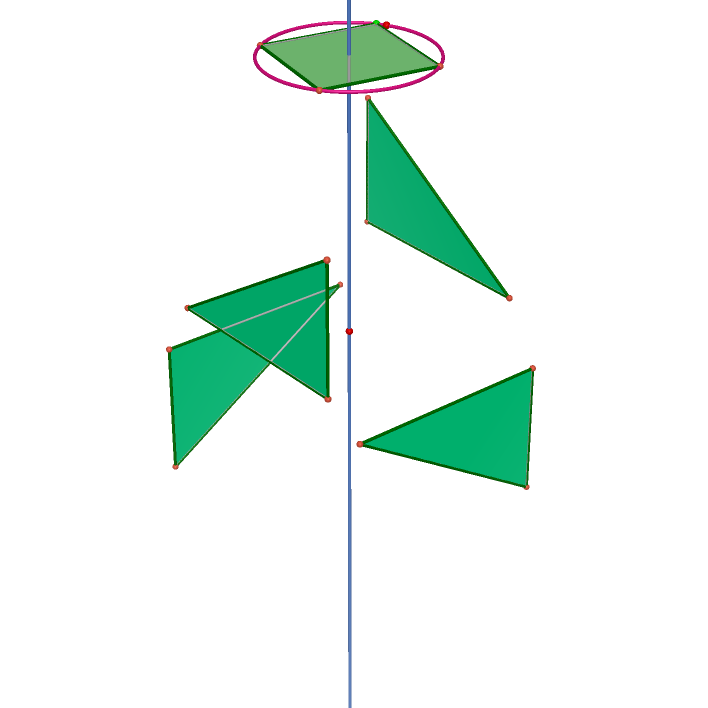
In order to describe the actions --- rotations and point reflections. The actions form a group, I define the <R_n> as the rotation around an axis through 360/n degrees, <O> as the point reflection through the center. I list all types of rotation groups and define equivalence classes if they are congruence by the same rotation group.
 |
 |
 |
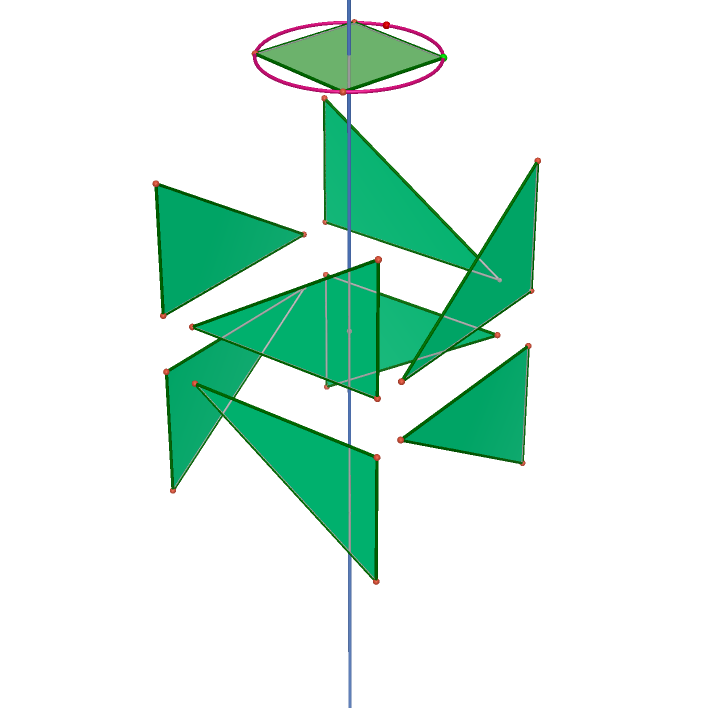 |
| <R_4> | <O> | <R_4 O> | <R_4,O> |
2.3 Classification of Faces
The projections of a polyhedron A on a polyhedron B are decided by the equivalence classes of the faces of A, so we have to understand the equivalence classes of faces of all Platonic solids.
| Platonic solids | faces | V | L | S |
| Tetrahedron | 4 | 1-1,<R_1> | 4-1,<R_4 O> | |
| 3-1,<R_3> | ||||
| Cube | 6 | 6-1,<R_3,O> | 2-1,<O> | 2-1,<O> |
| 4-1,<R_2,O> | 4-1,<R_4> | |||
| Octahedron | 8 | 8-1,<R_4,O> | 2-2,<O> | 2-1,<O> |
| 4-1,<R_2,O> | 6-1,<R_3,O> | |||
| Dodecahedron | 12 | 6-2,<R_3,O> | 2-2,<O> | 2-1,<O> |
| 4-2,<R_2,O> | 10-1,<R_5,O> | |||
| Icosahedron | 20 | 10-2,<R_5,O> | 2-2,<O> | 2-1,<O> |
| 4-4,<R_2,O> | 6-3,<R_3,O> |