多維期望值的討論
要進行討論之前,最重要的假設就是這些資料可以符合多維常態分布或是說沒有證據可以說資料不符合。回想我們在做單變量的推論前也是先要假設常態才能討論下去。在一維的時候有信賴區間(confidence interval),多變量也有對應的信賴域(confidence region)。但這邊的情況比單變量複雜得多,所以我們可以看到三種不同的信賴域。
第一種是對於期望值θpx1的信賴域。記成R(Xpx1),我們希望找到一個R(x) 使得
![]()
我們又知道
![]()
所以可以知道期望值的100(1-α)% 的信賴區是對所有的θpx1滿足下列式子
![]()
其中![]() 是樣本平均數,S樣本變異數。
是樣本平均數,S樣本變異數。
有時候我們有興趣的並不是所有變數的信賴域,在臨床實驗,我們會想看看不同治療的差異或是有時候我們有興趣的是一群變數加總和另一群變數加總的差異,簡單的說就是變數的線性組合。能包括對所有變數的線性組合的信賴區間,就是simultaneous confidence intervals。
現在我們有興趣的變數是Zj =a’Xj a: known
本來的變異數的估計值是樣本變異數,但現在的變數是Z,
![]()
所以只要把上面的樣本平均數和樣本變異數的部分換掉即可。如果只畫單一變數的simultaneous confidence interva的話,它會剛好切到confidence region的最外邊,可以看成是confidence region對該軸的投影。
![]()
Simultaneous CIs可以整個包住confidence region,所以它是比較保守的信賴區間。這是合理的,因為它的假設是要對“所有”的線性組合都對,所以會比較保守。如果我們不希望太保守還可以用Bonferroni method來造出比較有效率的信賴區間。
在同一個時候,我們其實並不需要所有的都對,只要看我們有興趣的信賴區間(記為Ci)就可以了。若我們想要得到所有的Ci(i=1..m)都對
![]()
若每個Ci可以分到α/m,單獨來看每個變數的CI
![]()
下面是一個模擬的例子:主要是生出一些獨立的normal 再給定相關性,畫出上面介紹的三種信賴域。
x=matrix(c(1,.5,.5,1),ncol=2) #二變數的cov matrix
e=eigen(x)$value; #算出共變異數矩陣的特徵值及向量
v=eigen(x)$vector
a=v%*%diag(sqrt(e))%*%t(v) #a=sqrt(x)
library(ellipse) #先安裝才能使用(畫橢圓)
n=50;p=2
y=matrix(rnorm(100),nrow=2) #生成獨立的normal r.vs 填到50×2的矩陣
![]()
ay=a%*%y #給一個y有x關係
varay=var(t(ay));
apply(t(ay),2,mean)
[1] -0.01626491 0.00868441
plot(ellipse(varay/n , level=.9,t=sqrt(p*(n-1)/(n-p)*qf(.9,p,n-p))),type="l",
lty=2,ylim=c(-3,4),xlim=c(-3,3),,col=2,xlab=””,ylab=””)
points(t(ay))
sci=sqrt(p*(n-1)/(n-p)*qf(.9,p,n-p))*sd(t(ay))
sci1=c(-1,1)*sci[1];
sci2=c(-1,1)*sci[2];
rect(sci1[1],sci2[1],sci1[2],sci2[2])
bci=qt(1-.05/2,n-1)*sd(t(ay))
bci1=c(-1,1)*bci[1];
bci2=c(-1,1)*bci[2];
rect(bci1[1],bci2[1],bci1[2],bci2[2],lty=3,lwd=2)
legend("topleft",c("confidence region","Simultanious CI","Boferroni method"),
lty=c(2,1,3),inset=.008,lwd=c(1,1,2),col=c(2,1,1))
text(locator(3),paste(1:3))
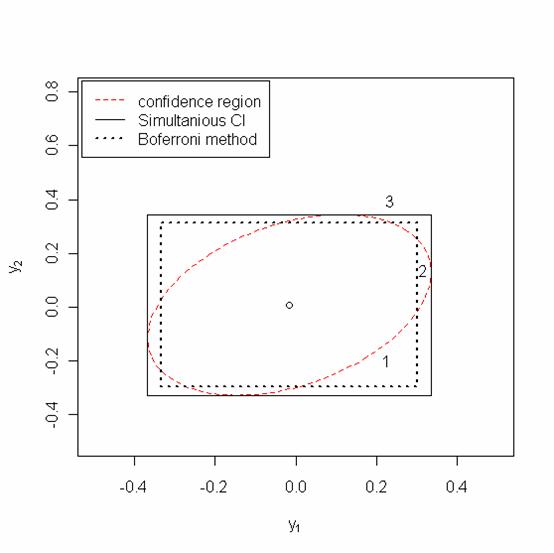
圖一
如果你收集到的資料發生在圖一#1或#2或#3,你會想怎麼解釋呢?
其實這三種最大的不同就是對於線性組合的假設,#1是不滿足confidence region但滿足另外兩個。Confidence region需要很強的線關係,他可以允許變異稍大於Bonferroni但是一定要在某一程度的相關。若有另一筆資料它的covariance是負的(就是再給它另一種線性關係),#1就會滿足它的confidence region。所以Simultaneous CIs是對所有的線性關係都要對才行。
關於這個部分還有單樣本及多樣本的檢定,可以參考Everitt 書上的第七章或是課本的第五章及第六章