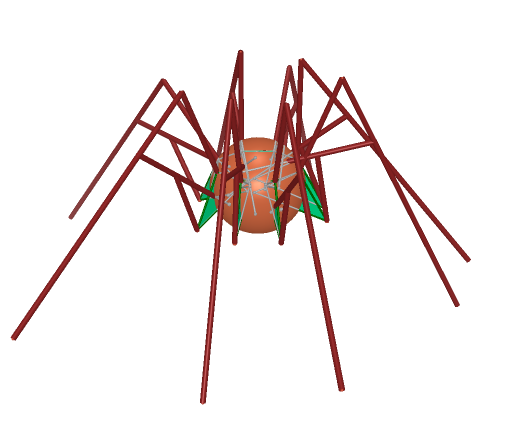
The Klann linkage is a planar mechanism designed to simulate the gait of legged animal and function as a wheel replacement. The linkage consists of the frame, a crank, two grounded rockers, and two couplers all connected by pivot joints.
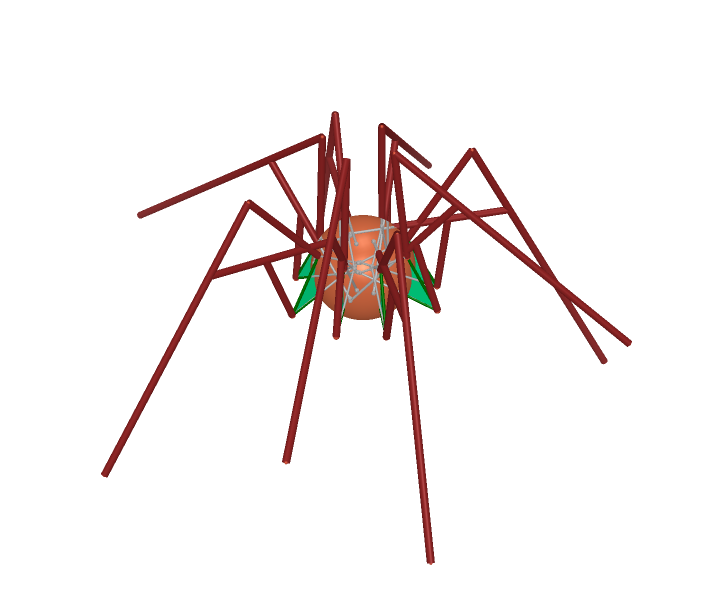
The picture above show the original model, and another has other four leg to make it more like a real spider. Click right pictures to see the animation. The following is a detailed construction process. There is not construction process of first picture since it is contained in the second one.
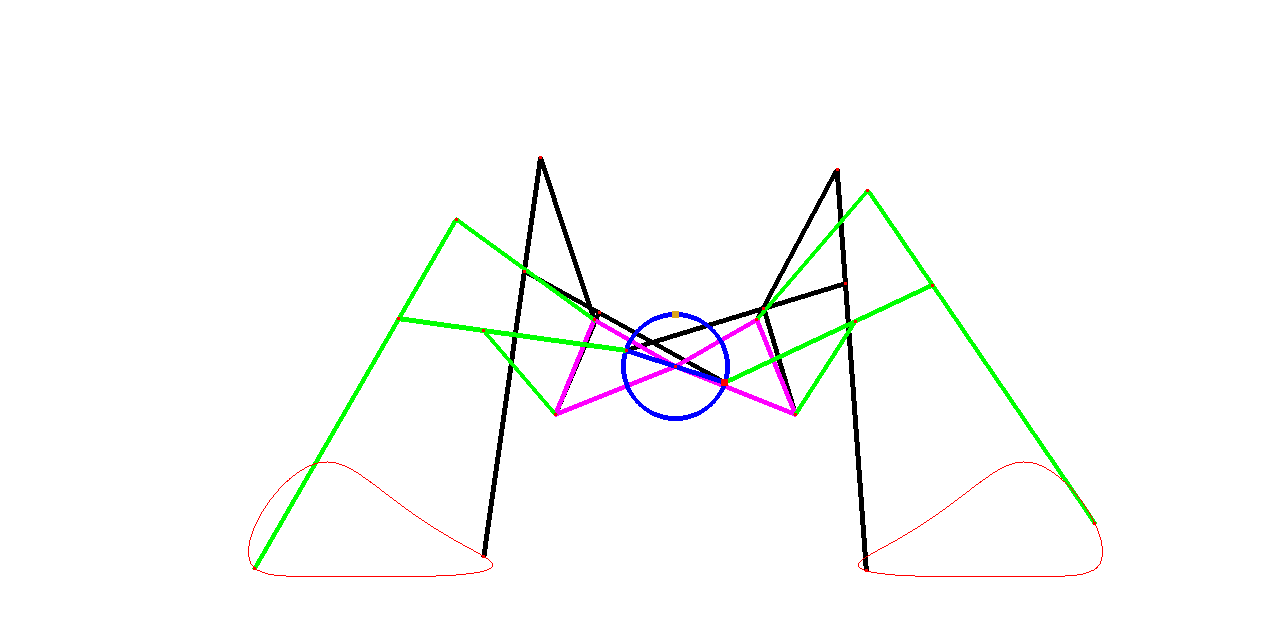
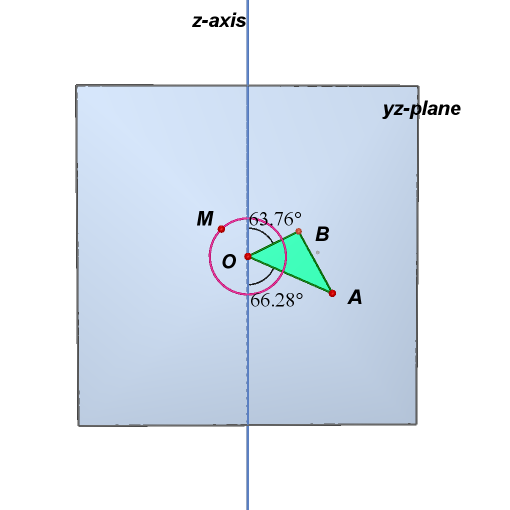
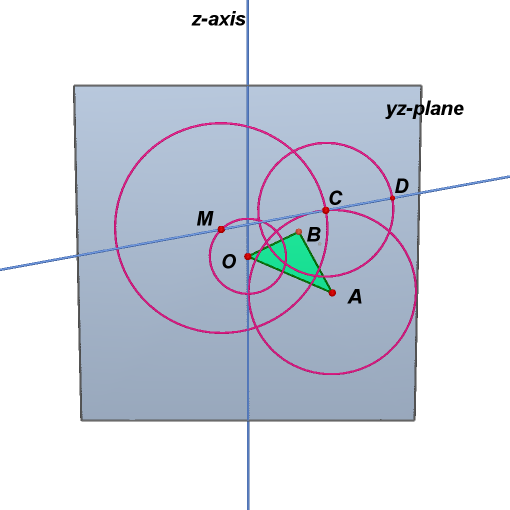
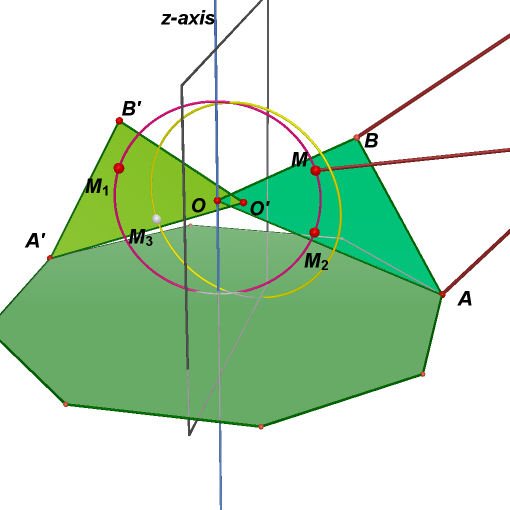
1. Start with a triangle
OAB in yz-plane where the angle between z-axis and segment OB is 63.76
degrees, the angle between z-axis and segment OA is 66.28 degrees, and
![]() =
0.611
=
0.611 ![]() .
.
2. Draw a circle in yz-plane centered on point O of radius 0.412
3. In yz-plane, draw
circle centered on M of radius 1.143
![]() and
circle centered on A of radius 0.909
and
circle centered on A of radius 0.909
![]() .
Point C is the intersection of the two circles.
.
Point C is the intersection of the two circles.
5. Hide previous three circles and line. Connect segment AC and MD.
6. In yz-plane, draw
circle centered on D of radius 0.93
![]() and
circle centered on B of radius 1.323
and
circle centered on B of radius 1.323
![]() .
Point E is the intersection of the two circles.
.
Point E is the intersection of the two circles.
7. Create a line through E
and D and a circle centered on D in yz-plane of radius 2.577
![]() .
Point F is their intersection.
.
Point F is their intersection.
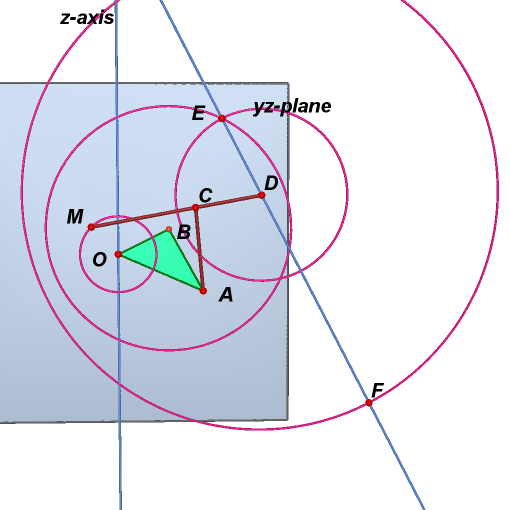
8. Hide previous three circles and line. Connect segment BE and EF.
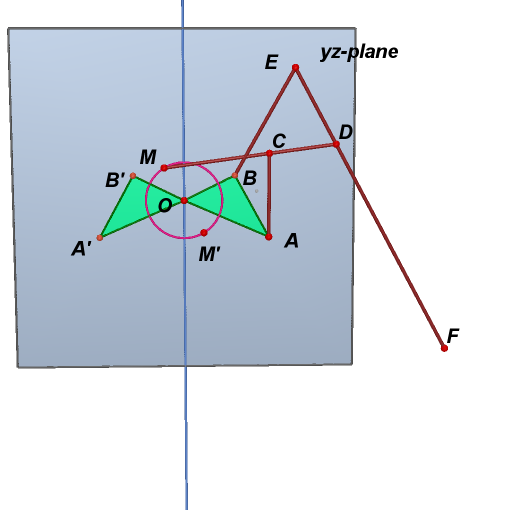
We say that the four segments AC, MD, BE, EF, and triangle OBA compose the first leg.
9. Point M' is the central symmetry of point M through point O. Triangle OA'B' is the half-turn of triangle OAB around z-axis.
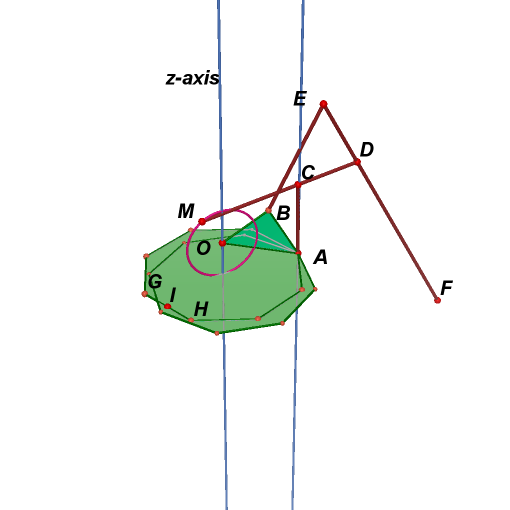
10. Hide yz-plane. Draw a regular octagon around z-axis through point A. Point G and H are adjacent vertices in the regular octagon, and point I is their midpoint.
11. Create a line parallel z-axis through point A. Rotate previous regular octagon around this line mapping point G to point I to obtain another regular octagon.
12. Hide the original regular octagon.
13. Create a plane bisecting the remaining regular octagon. Reflect triangle OAB and remaining circle in this plane to obtain a new triangle O'A'B' and a new circle.
14. Point
15. Hide the bisecting
plane. Repeat steps 3~7 to point
![]() and
triangle O'A'B'.
and
triangle O'A'B'.
16. Create another
bisecting plane of regular octagon. Reflect two triangles and two
circles to obtain two new triangles and circles. Call the two vertices
of the triangle in the circle
![]() ,
,
![]() .
.
17. Translate point M mapping point O to
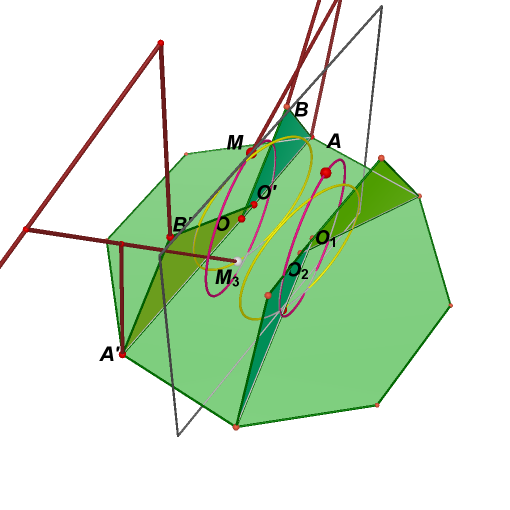
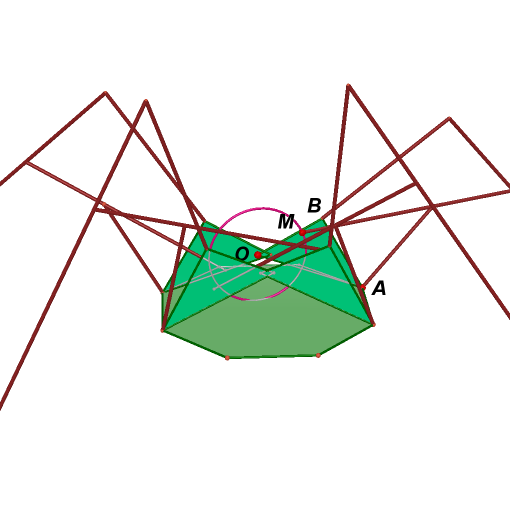
19. For convenience, we leave the first leg, and hide three other legs temporarily.
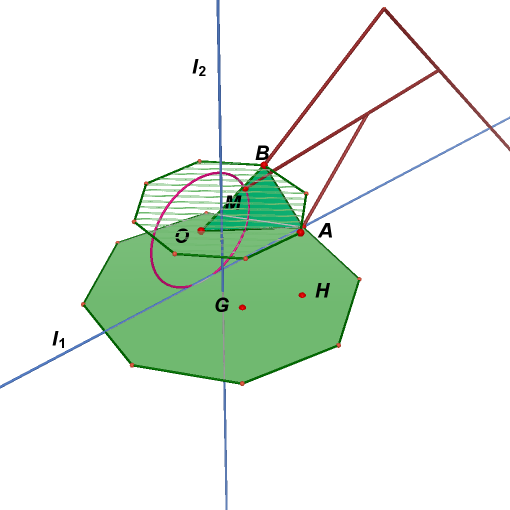
20. Create a line
![]() which
is the intersection of the plane containing regular octagon and the
plane containing triangle OAB. Rotate point O and M 90 degrees
counterclockwise around this line to obtain point G and H.
which
is the intersection of the plane containing regular octagon and the
plane containing triangle OAB. Rotate point O and M 90 degrees
counterclockwise around this line to obtain point G and H.
21. Create a line
![]() perpendicular
to regular octagon through its center. Draw a new regular octagon around
this line through point B.
perpendicular
to regular octagon through its center. Draw a new regular octagon around
this line through point B.
22. Point I is a vertex of
new regular octagon obtained from rotating point B around line
![]() clockwise
90 degrees. Create a line
clockwise
90 degrees. Create a line
![]() through
point I and center of new regular octagon.
through
point I and center of new regular octagon.
23. Take a point J on line
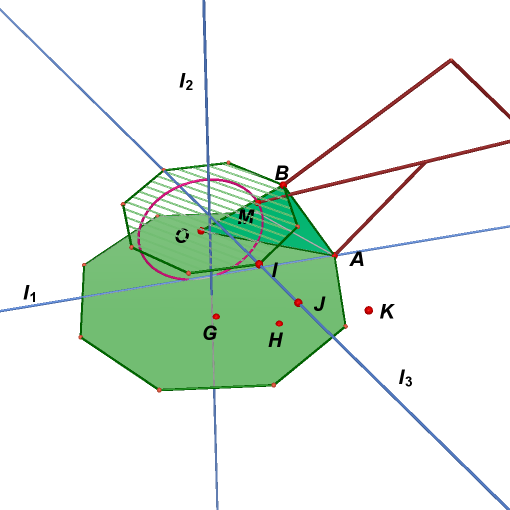
24. Hide point G, point H,
line
![]() ,
and bigger regular octagon.
,
and bigger regular octagon.
25. Create two line in the
plane containing smaller regular octagon. One is perpendicular to line
![]() through
point J, and another is parallel to line
through
point J, and another is parallel to line
![]() through
point K. Call the intersecting point of two lines L.
through
point K. Call the intersecting point of two lines L.
26. Draw a line
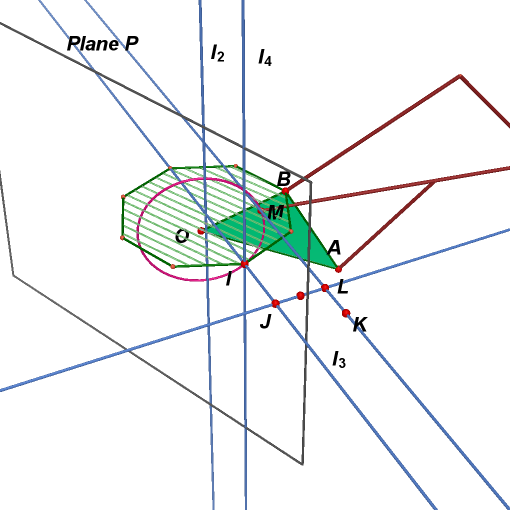
27. Hide point J, K, L,
line
![]() ,
and two line at step 22.
,
and two line at step 22.
28. Translate point M and
triangle OBA to obtain point ![]() and
a new triangle. Point A'' is the vertex of new triangle corresponding to
point A.
and
a new triangle. Point A'' is the vertex of new triangle corresponding to
point A.
29. Rotate point
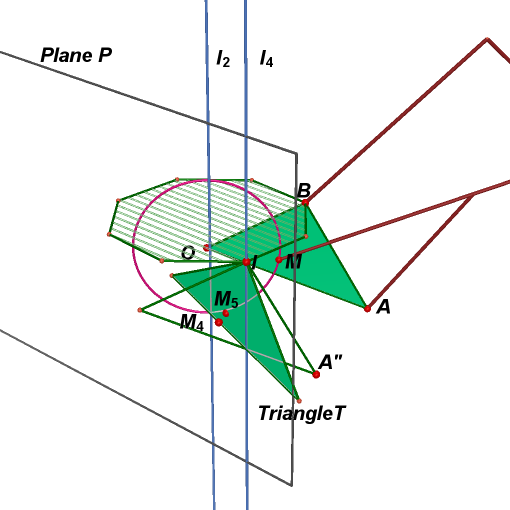
30.
Hide point
![]() ,
line
,
line
![]() ,
and triangle containing point A''. Repeat steps 3~7 to point
,
and triangle containing point A''. Repeat steps 3~7 to point
![]() and
triangle T.
and
triangle T.
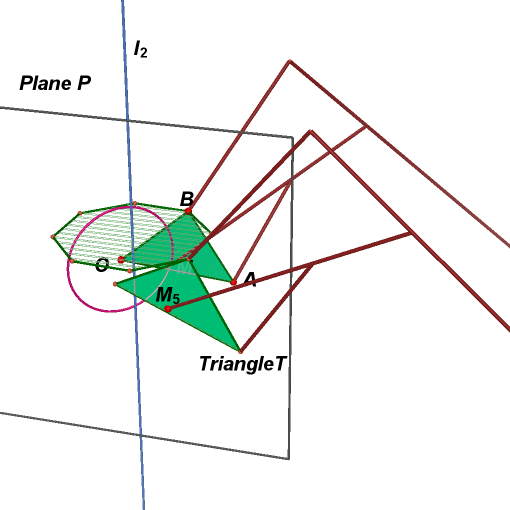
31. Create a plane
containing line
![]() and
through point B. Reflect point
and
through point B. Reflect point
![]() and
triangle T in this plane to obtain point
and
triangle T in this plane to obtain point
![]() and
a new triangle T'. Also reflect plane P in this plane to obtain plane
P'.
and
a new triangle T'. Also reflect plane P in this plane to obtain plane
P'.
32. Draw a line parallel
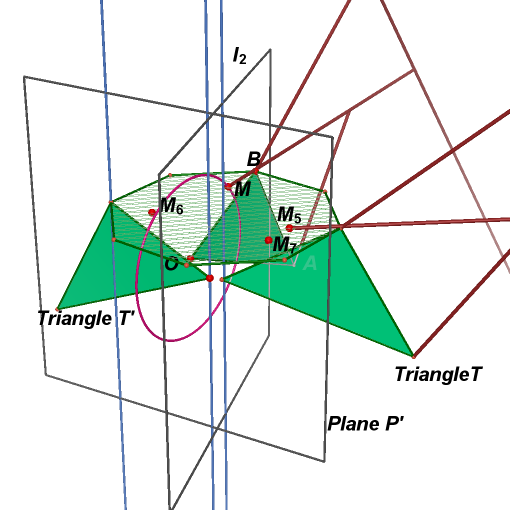
33. In plane P', repeat
steps 3~7 to point
![]() and
triangle T'. Hide useless objects.
and
triangle T'. Hide useless objects.
34. Rotate plane P',
triangle T' and point
![]() around
line
around
line
![]() 135
degrees counterclockwise to obtain plane P'', triangle T'' and point
135
degrees counterclockwise to obtain plane P'', triangle T'' and point
![]() .
.
35. Take a point
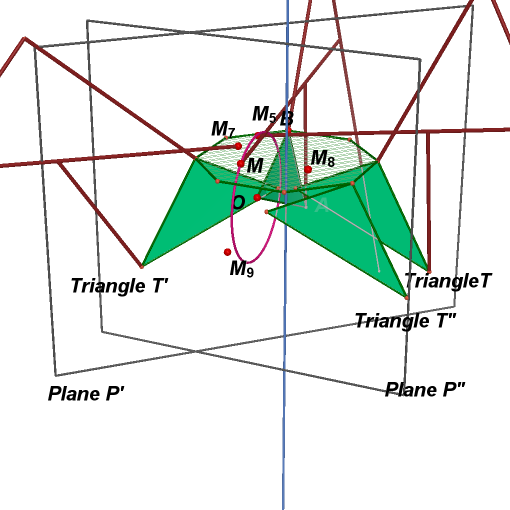
36. In plane P'', repeat
steps 3~7 to point
![]() and
triangle T''. Hide the useless objects.
and
triangle T''. Hide the useless objects.
37. Create a plane perpendicular line
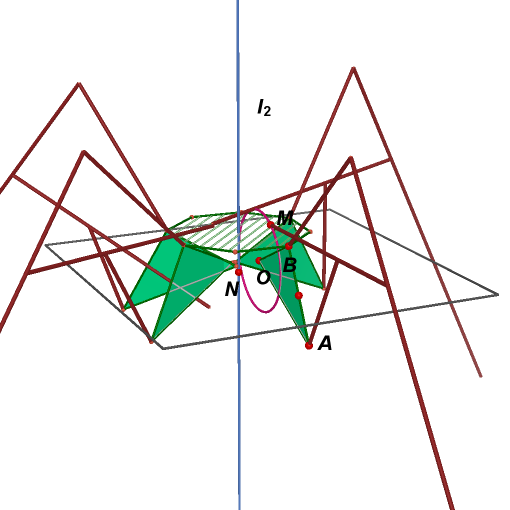
38. Repeat steps 31~32 to
point
![]() and
triangle T to obtain final leg.
and
triangle T to obtain final leg.
39. Show previous hidden three leg. Draw a sphere centered on point N through point B.