主成份分析
主成份分析(PCA)主要是想要用比較少的「成份」來看資料變異的來源(也就是降低資料的維度)。主成份分析是因子分析的一個特例,但主成份分析想看的是造成資料變異的結構,而因子分析想看的是資料裡變數之間的關係。
這些成份是由原來資料變數的線性組合所造出來,當然並不是所有的線性組合都可以,不然係數愈大,所造出的來的線性組合的變異也愈大,必須對係數加入限制,每一個主成份的係數的向量,長度為1。另外我們也不希望各主成份之間會互相影響,所以不同主成份的內積是0。我們希望主成份可以降低資料的維度,所以只要挑比較大的幾個主成份就足夠解釋。這樣一來資料的維度就會降低,而又可以達到需要解釋的水準。
先想一個極端的例子,如果資料裡面有五個變數,2nd~5th 都是1st的倍數,那我們需要把所有的變數都放到模型裡去?其實這份資料的變異來源就只有第一個變數。在有高度線性相關的變數,用主成份去做分析會比用原來的變數做分析來得恰當。
根據這些性質,在矩陣運算上所使用的特徵值和特徵向量會符合這些特性。我們就採用這種方法來做主成份分析(PCA)。

現在用一個例子來看,先把Fertility的資料扣起來,待拿來做迴歸。
data(swiss) #資料在R的data set
S=var(swiss[,-1]) #把Fertility的資料扣起來
pca=princomp(swiss[,-1])#丟資料
names(pca)
summary(pca)
|
|
Comp.1 |
Comp.2 |
Comp.3 |
Comp.4 |
Comp.5 |
|
Standard deviation |
42.896 |
21.202 |
7.588 |
3.688 |
2.721 |
|
Proportion of Variance |
0.777 |
0.190 |
0.024 |
0.006 |
0.003 |
|
Cumulative Proportion |
0.777 |
0.967 |
0.991 |
0.997 |
1.000 |
pld=pca$loading
fix(pld)
#比較一下,特徵值、特徵向量和PCA做出來的東西#
e=eigen(S)$vecto r #特徵向量
v=eigen(S)$value #特徵值
#---特徵向量e的部分----(有時會差一個負號)#
pld
|
|
Comp.1 |
Comp.2 |
Comp.3 |
Comp.4 |
Comp.5 |
|
Agriculture |
0.282 |
0.884 |
-0.37 |
-0.027 |
-0.049 |
|
Examination |
-0.121 |
-0.174 |
-0.45 |
-0.867 |
0.033 |
|
Education |
-0.058 |
-0.311 |
-0.807 |
0.485 |
-0.117 |
|
Catholic |
0.95 |
-0.303 |
0.002 |
-0.071 |
0.022 |
|
Infant.Mortality |
0.01 |
-0.019 |
0.099 |
-0.087 |
-0.991 |
e
|
|
[,1] |
[,2] |
[,3] |
[,4] |
[,5] |
|
[1,] |
0.282 |
0.884 |
0.37 |
-0.027 |
-0.049 |
|
[2,] |
-0.121 |
-0.174 |
0.45 |
-0.867 |
0.033 |
|
[3,] |
-0.058 |
-0.311 |
0.807 |
0.485 |
-0.117 |
|
[4,] |
0.95 |
-0.303 |
-0.002 |
-0.071 |
0.022 |
|
[5,] |
0.01 |
-0.019 |
-0.099 |
-0.087 |
-0.991 |
#---特徵值v的部分------#
sqrt(v) #summary出來的是Sd
|
43.360 |
21.431 |
7.670 |
3.728 |
2.751 |
v/sum(v)
|
0.777 |
0.19 |
0.024 |
0.006 |
0.003 |
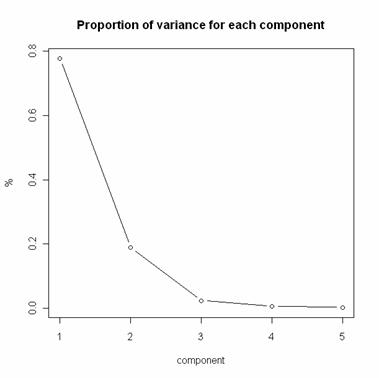
圖一:各主成份所解釋的變異百分比
由圖一可以看出選擇二個主成份即可,在第三主成份有一個折點。第三個主成份之後就只有很小的貢獻。特徵值的部分可以和前面的summary(pca)比較,特徵值會有一點不一樣,但是變異數的比例是和特徵值算出來的一樣。
現在來看我們做出來的主成份。第一個主成份是和Catholic及Infant.Mortality有關,第二個主成份是和Agriculture Education Catholic有關等等。有時候我們可以藉由主份份來將變數來分群,賦予新的意義,但這邊看來,似乎和原本的變數較接近,每一個主成份有極大的比例是在某一個變數上面。所以主成份的順序可以看成是變數重要性的次序。Catholic這樣來看,是資料swiss[,-1]中最重要的變數。
比較奇怪的是這個。照理說,用主成份來做迴歸應該是愈前面的主成份配適得愈好,因為它已經代表predictors大部份的變異,但結果似乎並不是這樣。
mod=lm(swiss[,1]~pca$score[,1:3]) #用前面三個主成份做的model
summary(mod)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 70.14255 1.10854 63.275 < 2e-16 ***
pca$score[, 1] 0.14376 0.02584 5.563 1.57e-06 ***
pca$score[, 2] 0.11115 0.05228 2.126 0.0393 *
pca$score[, 3] 0.98882 0.14609 6.769 2.79e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.6 on 43 degrees of freedom
Multiple R-squared: 0.654, Adjusted R-squared: 0.6299
F-statistic: 27.09 on 3 and 43 DF, p-value: 5.357e-10
mod1=lm(swiss[,1]~pca$score[,1:2]) #另一個比較小的model
Call:
lm(formula = swiss[, 1] ~ pca$score[, 1:2])
….
Residual standard error: 10.8 on 44 degrees of freedom
Multiple R-squared: 0.2854, Adjusted R-squared: 0.2529
F-statistic: 8.786 on 2 and 44 DF, p-value: 0.000616
cor(cbind(swiss[,1],pca$score))[2:6,1]
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
0.499 0.191 0.607 -0.088 -0.212
這是Fertility和其它主成份的相關係數,看起來,第二主成份並不是很相關。這樣的結果是對的?
因為主成份只有解釋那一些我們丟進去的資料。由那些資料變數的線性組合生成新的主成份,所以和我們沒有丟進去的資料並不一定相關,當然原來資料可以解釋的部分用全部的主成份下去也是一樣。所以可能較前面的主成份並不一定可以對Fertility有很好的解釋。除非Fertility變異的方式和我們丟進去資料的變異很相似。
也許看一下pairs plot 會有其它的想法。
pairs(swiss, panel = panel.smooth, main = "swiss data",
col = 3 + (swiss$Catholic > 50))
藍色和綠色的表現是不是很不一樣?所以,Catholic是一個很重要的變數。
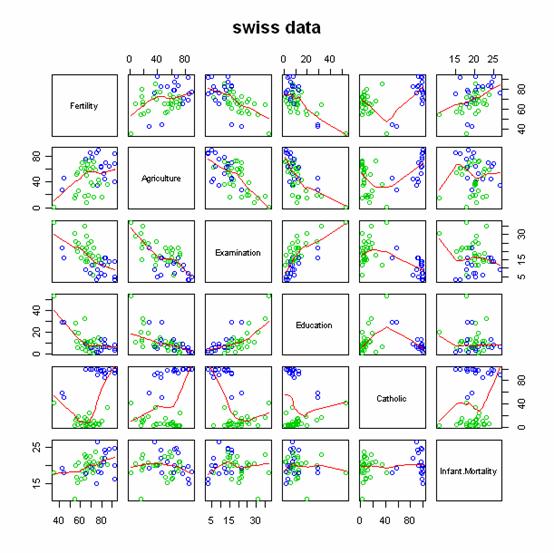
圖二:藍色的部分是天主教比例較高的地區